안녕하세요 이번 시간에는 넘파이를 이용할때마다 자주보는 axis, keepdims!
하지만 할때마다 헷갈리는 두녀석을 완벽하게 이해하는 시간을 가져보고자 합니다.
"axis = 0" 과 "axis =1" | np.sum() 연산
1. axis = 0일 때
import numpy as np
a= np.arange(12).reshape((3,-1)) # 3행으로만들고 나머지는 원소갯수에 따라 알아서 맞추라고 지정.
sum_ = a.sum(axis=0) # np.sum(a,axis=0)이랑 같음
print("ndarray: {}\n{}".format(a.shape, a))
print("ndarray.sum(axis=0): {}\n{}".format(sum_.shape,sum_))output :
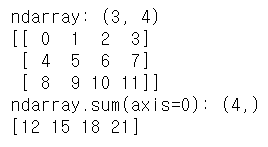
2. axis = 1일 때
import numpy as np
a= np.arange(12).reshape((3,-1)) # 3행으로만들고 나머지는 원소갯수에 따라 알아서 맞추라고 지정(-1)
sum_ = a.sum(axis=1) # np.sum(a,axis=1)이랑 같음
print("ndarray: {}\n{}".format(a.shape, a))
print("ndarray.sum(axis=0): {}\n{}".format(sum_.shape,sum_))output :

두 결과를 보시면 아 axis = 0 , 1일때 어떤 방향으로 연산이 되는지 감이 오실겁니다.
그림을 통해 무엇을 중요시 봐야하는지 다시한번 보죠!
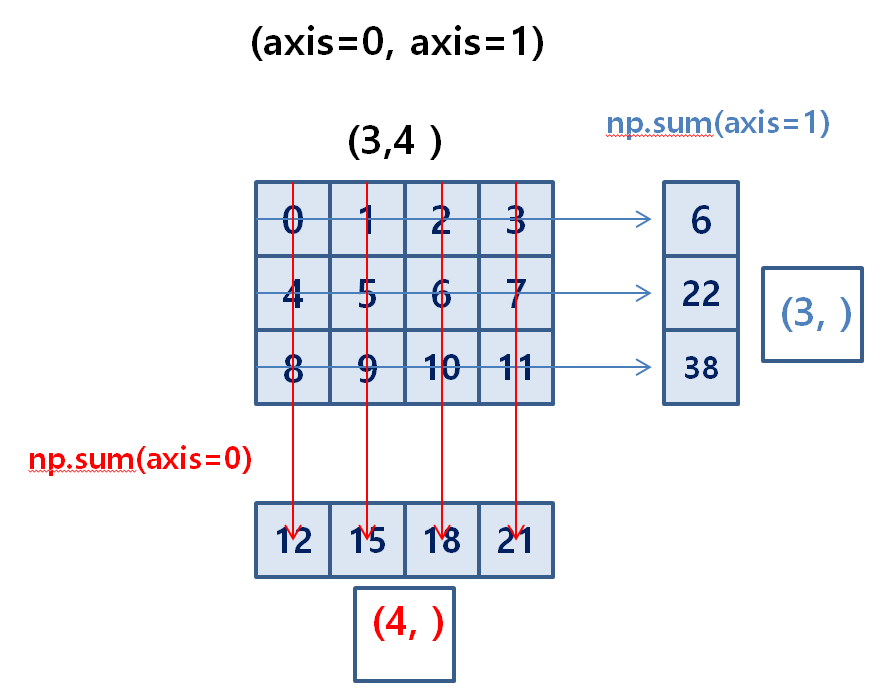
axis =1 은 파란선방향 axis = 0은 빨간색 방향으로 연산을 합니다.
이때 axis =1 을 통해 연산을 한 결과의 shape을 주목해주십시오!
어떤가요? 2차원에서 1차원으로 차원이 한 차원 downgrade 되었네요!
그리고 (3,4) 에 column 부분이 없어졌습니다.
aixs = 0은 빨간색 방향으로 연산을 합니다.
그리고 연산을 통한 결과의 shapedms (4,) 로 (3,4)에서 3 부분 즉 row부분이 날아갔군요..
정리하자면, row 방향으로 연산(axis=0)을 할땐 row 부분(여기선 3)이 사라지고 column 방향으로 연산(axis=1)을 할때는 column의 숫자(여기선 4)가 사라지는 것을 확인 할 수 있네요! 조금만 생각하면 당연한거지만 차원이 커지면 헷갈릴 수 있으니 머리에 잘 넣어두시면 좋겠습니다.
+ 보너스
axis = 0, axis=1 도대체 어느 방향으로 연산하는거지? 라고 자주 헷갈리시는 분들은 이렇게 외워주시면 좋겠습니다!
위 예시만 보고 아 axis = 0 은 row 방향이고 axis = 1은 column 방향이다라고 외우시기보다 저는 이런방식을 추천드립니다.
"axis = 0 이 가장 바깥차원 방향 axis = 1 이 그 다음 차원방향이다." 라고 외워 주시면 좋겠습니다.
이게 무슨 말이냐구요?
(2,3) 행렬이 있다고 합시다.
여기서 (2,3)은 (3,) 벡터가 2개 있는 것을 의미합니다.
즉 2가 3보다 더큰 차원의 개념이죠?
(3,2,4)의 텐서가 있다고 합시다.
이건 풀어서 설명하면
(4,)의 벡터가 2개 있는데 ===> (2,4)
근데 그녀석(2,4)이 3개가 있다는 말입니다. ====> (3,2,4)
즉 3이 가장 바깥차원의 수 , 2가 그 다음 , 4가 가장 안쪽 차원의 갯수이겠지요?
이제 어느정도 감이 잡히셨을 겁니다.
axis = 0 일때 row 방향이라는건 2차원일때만 해당되는이야기입니다.
3차원에서 axis = 0 즉 제일 바깥 차원이 뭐죠? 채널입니다. 그렇기 때문에 채널의 방향으로 연산이 됩니다.
아래와 같이 말이죠.

참고로 axis = 0하고 axis = 1만 있는게 아닙니다.
차원이 커지면 axis = 3, 4, 5 가 있을수도 있겠죠?
브로드캐스팅
axis 가 연산을 하기 위해 존재하므로 넘파이의 대표적인 연산 기술인 브로드캐스팅과는 뗄레야 뗄수 없는 관계입니다.
하지만 위에서 말씀드린대로 axis 를 통해 연산을하면 한차원이 다운그레이드되면서 shape의 모양이 바뀌게 됩니다.
앞선 브로드캐스팅 연산 2편 포스팅에서 말씀드린것처럼 차원이 다를경우 브로드캐스팅이 될때가있고 안될때가 있는데요.
위의 그림을 다시 한번 보겠습니다.

브로드캐스팅 편을 보신분은 알겠지만 axis = 1로 연산을 했을경우 브로드캐스팅 연산이 불가능합니다.
연산을 하려고하면 아마도 아래와 같은 "ValueError : operands could not be broadcast ..." 오류를 만나게될겁니다.

하지만 저 친구를 가지고 우리는 연산을 하고싶습니다..
어떻게 해야할까요? (3,)를 (3,1)로 변경해주면됩니다. 즉 차원을 맞춰주는것이지요.
이것에 대한 자세한 연산법은 브로드캐스팅 연산 1편에서 자세히 설명하였으니 참고바랍니다.
하지만 매번 차원을 바꿔주기 귀찮으니 이때 사용하는 것이 바로 keepdims입니다.
keepdims 사용
import numpy as np
a= np.arange(12).reshape((3,-1))
print("ndarray: {}\n{}".format(a.shape, a))
sum_class = np.sum(a, axis=0, keepdims=True)
sum_student = np.sum(a, axis=1 , keepdims=True)
print("sum_class: {}\n{}".format(sum_class.shape,sum_class))
print("sum_student): {}\n{}".format(sum_student.shape,sum_student))
output :

사용법은 연산하고자하는 함수 안에 keepdims = True로 설정해주시면 됩니다.
보시는것처럼 벡터의 [] 하나씩 더 추가되면서 행렬 즉 2차원이 된것을 보실 수 있습니다.

위 그림을 보시면 keepdims 를 적용하자 차원이 죽으면서 사라졌던 부분이 숫자 1로 바뀌면서 shape과 관계 없이 브로드캐스팅이 가능한 상태가 되었네요!
3차원 텐서 적용(axis =1 적용)
조금더 고차원으로 넘어가서 지금 까지 배운 내용을 적용해 보겠습니다.
먼저 문제를 하나 내겠습니다.!
(2,3,4)의 텐서가 있다고 합시다.
그런데 우리는 axis =1 을 적용해서 sum()를 이용해 연산을 한값을 sum_ 이라고 합시다.
이 sum_은 (2,3,4)와 브로드캐스팅이 가능할까요?
정답부터 말하자면 '불가능' 입니다
왜그럴까요?
앞서 설명드린대로 3차원에서 axis =1 방향으로 연산이란 row 방향 연산을 의미합니다.
다시말하면 row 방향의 숫자가 죽어서
(2,3,4) --> (2,4)의 형태로 됩니다.
(제가 왜 계속 위에서 차원과 shape을 강조했는지 이해가 되실겁니다.
이 부분이 이해가 안되시면 위에가서 다시한번 읽어보세요! 고차원이 될 수록 더 헷갈리니까요.)
그런데!
여기서 (2,4)의 shape을 가진 sum_ 이 과연 (2,3,4)와 연산이 가능할까요?
불가능합니다. 바로 이때 사용하는게 keepdims 입니다.
코드를 통해 확인하겠습니다.
import numpy as np
a = np.arange(2*3*4).reshape((2, 3, 4))
sum_ = a.sum(axis=1)
sum_k = a.sum(axis=1, keepdims =True)
print("ndarray: {}\n{}".format(a.shape, a))
print("axis=1: {}\n{}".format(sum_.shape, sum_)) # 이건 브로드캐스팅 불가능
print("axis=1, keepdims=True: {}\n{}".format(sum_k.shape, sum_k)) #이건 브로드 캐스팅 가능output :

keepdims를 True로 설정하니 사라졌던 부분이 다시 1로 생겼네요.
차원이 같아졌고 가운데 1이 있으니 브로드캐스팅이 가능합니다.
3차원 텐서 적용(axis =2 적용)
import numpy as np
a = np.arange(2*3*4).reshape((2, 3, 4))
sum_ = a.sum(axis=2)
sum_k = a.sum(axis=2, keepdims =True)
print("ndarray: {}\n{}".format(a.shape, a))
print("axis=1: {}\n{}".format(sum_.shape, sum_))
print("axis=1, keepdims=True: {}\n{}".format(sum_k.shape, sum_k))이번엔 위코드에 axis =2 를 적용해볼게요
그럼 연산한 sum_이 어떤 shape이 될까요?
axis = 0 도아니고 1도 아니고 2이니..
3차원에서 가장 안쪽인 column 방향으로 연산 한다는 뜻이네요.
column을 나타내는 4가 사라진 (2,3)이 sum_의 shape이 됩니다.
output :

하지만 (2,3)은 (2,3,4)와 브로드캐스팅 연산이 안되니 kepdims = True를 통해 shape을 변경해줍니다.
역시 마찬가지로 사라졌던 4자리가 1로 바뀌었네요!
정리
이번 시간에는 axis 의 방향에 따라 어떻게 shape이 바뀌게되고,
또 그 shape을 keepdims 를 이용해서 브로드 캐스팅 까지 알아보았습니다.
이 글과 읽으면 좋은글
'머신러닝,딥러닝 > 넘파이,numpy' 카테고리의 다른 글
| [넘파이 기초] bool ndarray로 인덱싱하기(np.nonzero, np.where) (0) | 2021.04.28 |
|---|---|
| [넘파이 기초] 반올림, 올림, 버림 (0) | 2021.04.27 |
| [넘파이 기초] int ndarray로 인덱싱 (indexing) 하기 (0) | 2021.04.22 |
| [넘파이 기초] broadcasting(브로드 캐스팅) 파헤치기 2편 (0) | 2021.04.17 |
| [넘파이 기초] broadcasting(브로드 캐스팅) 파헤치기 1편 (0) | 2021.04.16 |






댓글